Notes on "Neural Ordinary Differential Equations"
前言
这篇18年Neurlps的bestpaper,主要的卖点在于改进了以往网络随着深度增加所需求的内存不断增多的问题,通过求解常微分方程的形式,在不储存中间状态的情况下,计算出网络的最终输出,将神经网络控制在了常数级的内存消耗(与网络深浅无关)。
Insight
常微分方程我们都学过,怎么解析求解、存在性定理、唯一性定理、渐近性质等等,在数值计算课上也学过一些数值求解算法。无论做什么,想法都很重要。
许多网络模型中,前馈过程都使用了迭代形式,如残差网络: \[ \mathbf{h}_{t+1}=\mathbf{h}_{t}+f\left(\mathbf{h}_{t}, \theta_{t}\right) \] 这可以看作前向欧拉迭代求解微分方程的过程,将层数作为变量,取步距为一。如果还原为最原始的形式,即允许连续层数: \[ \frac{d \mathbf{h}(t)}{d t}=f(\mathbf{h}(t), t, \theta) \] 那么这篇文章的标题NeuralODE就很好理解了,整个神经网络表示了一个微分方程,求解微分方程的过程即为推理过程。同时,\(\textbf{h}(0)\)即为网络的输入,给定了微分方程的初值,一个黑盒求解器可以为我们求出方程解在任意时刻T的函数值\(\textbf{h}(T)\).
细节
文章的insight并不难以理解,这个想法是完全可行的,剩下的问题集中在如何对网络进行训练,使方程的解正好是我们想要的结果。由于在处理方程求解器时,作者完全将其作为黑盒,所以这一步操作是不可微的,无法计算梯度。作者这里使用了adjoint sensitivity method,用于计算梯度,它是线性规模的算法,消耗内存较小。
考虑给定的损失函数\(L(\cdot)\),它对方程解在最终时刻的函数值进行度量(即推断结果):
\[ L\left(\mathbf{z}\left(t_{1}\right)\right)=L\left(\mathbf{z}\left(t_{0}\right)+\int_{t_{0}}^{t_{1}} f(\mathbf{z}(t), t, \theta) d t\right)=L\left(\text { ODESolve }\left(\mathbf{z}\left(t_{0}\right), f, t_{0}, t_{1}, \theta\right)\right) \] 我们的目的是求解 \(\frac{\partial L}{\partial \theta}\) . 按照adjoint sensitivity method的流程,我们需要先求解一个叫adjoint的函数\(\mathbf{a}(t)=\partial L / \partial \mathbf{z}(t)\),它被定义为损失对隐藏状态\(\mathbf{z}(t)\)的梯度,这听起来好像更困难了一些,好在adjoint满足另一个微分方程: \[ \frac{d \mathbf{a}(t)}{d t}=-\mathbf{a}(t)^{\top} \frac{\partial f(\mathbf{z}(t), t, \theta)}{\partial \mathbf{z}} \] 证明先省略,只要求解这个ODE,我们就能够得到adjoint. 考虑反向传播的流程,只有终值是知道的,这个方程需要从$ t_1$开始求解。除此之外,求解这个ODE还需要知道 $ (t)$ 的数值,但我们知道网络最终的输出$ (t_1)$,以此为初值,重新求解神经网络构成的微分方程即可。
知道adjoint后,最后的一步就是求解 \(\frac{\partial L}{\partial \theta}\) ,这需要再次计算一个积分,它与 $ (t),(t)$ 都有关: \[
\frac{d L}{d \theta}=\int_{t_{1}}^{t_{0}} \mathbf{a}(t)^{\top} \frac{\partial f(\mathbf{z}(t), t, \theta)}{\partial \theta} d t
\] 证明先省略,上面过程中出现的 \(\textbf{a}(t)^T\frac{\partial f}{\partial z},\textbf{a}(t)^T\frac{\partial f}{\partial \theta}\)都可以由深度学习框架的自动微分快速计算。最后一个问题是,最终的损失可能与$ (t)$某个特定的中间状态相关。这也很容易解决,只要逐段地进行上面的流程即可,以上次的结果作为初值,如下图所示: 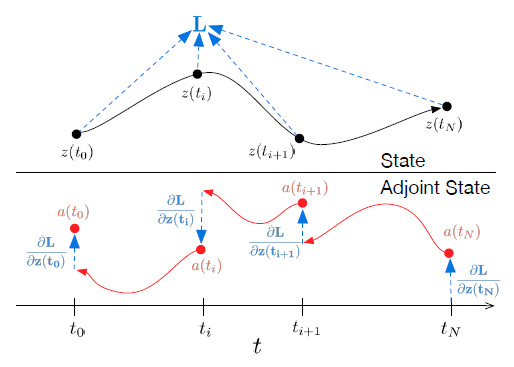 后面的我不准备仔细展开,说一下大致的实验结果。在MNIST上达到了0.42%的错误率,作为对比的ResNET错误率为0.41%.
后面的我不准备仔细展开,说一下大致的实验结果。在MNIST上达到了0.42%的错误率,作为对比的ResNET错误率为0.41%.
证明环节
第一个要证明adjoint确实满足另一个微分方程。为简易起见,这里的向量都为行向量,正文中的是列向量。
\[ \frac{d \mathbf{z}(t)}{d t}=f(\mathbf{z}(t), t, \theta) \]
\[ \mathbf{a}(t)=\frac{d L}{d \mathbf{z}(t)} \]
需证: \[ \frac{d \mathbf{a}(t)}{d t}=-\mathbf{a}(t)^{T} \frac{\partial f(\mathbf{z}(t), t, \theta)}{\partial z} \] 在 \(\epsilon\)时刻后,隐状态的改变如下:
\[ \mathbf{z}(t+\epsilon)=\int_{t}^{t+\epsilon} f(\mathbf{z}(t), t, \theta) d t+\mathbf{z}(t)=T_{\epsilon}(\mathbf{z}(t), t) \] 由链式法则:
\[ \frac{d L}{d \mathbf{z}(t)}=\frac{d L}{d \mathbf{z}(t+\epsilon)} \frac{d \mathbf{z}(t+\epsilon)}{d \mathbf{z}(t)}, \mathbf{a}(t)=\mathbf{a}(t+\epsilon) \frac{d T_{\epsilon}(\mathbf{z}(t), t)}{d \mathbf{z}(t)} \] 由导数定义 \[ \begin{aligned} \frac{d \mathbf{a}(t)}{d t} &=\lim _{\varepsilon \rightarrow 0^{+}} \frac{\mathbf{a}(t+\varepsilon)-\mathbf{a}(t)}{\varepsilon} \\ &=\lim _{\varepsilon \rightarrow 0^{+}} \frac{\mathbf{a}(t+\varepsilon)-\mathbf{a}(t+\varepsilon) \frac{\partial}{\partial \mathbf{z}(t)} T_{\varepsilon}(\mathbf{z}(t))}{\varepsilon} \\ &=\lim _{\varepsilon \rightarrow 0^{+}} \frac{\mathbf{a}(t+\varepsilon)-\mathbf{a}(t+\varepsilon) \frac{\partial}{\partial \mathbf{z}(t)}\left(\mathbf{z}(t)+\varepsilon f(\mathbf{z}(t), t, \theta)+\mathcal{O}\left(\varepsilon^{2}\right)\right)}{\varepsilon} \\ &=\lim _{\varepsilon \rightarrow 0^{+}} \frac{\mathbf{a}(t+\varepsilon)-\mathbf{a}(t+\varepsilon)\left(I+\varepsilon \frac{\partial f(\mathbf{z}(t), t, \theta)}{\partial z(t)}+\mathcal{O}\left(\varepsilon^{2}\right)\right)}{\varepsilon} \\ &=\lim _{\varepsilon \rightarrow 0^{+}} \frac{-\varepsilon \mathbf{a}(t+\varepsilon) \frac{\partial f(\mathbf{z}(t), t, \theta)}{\varepsilon \mathbf{z}(t)}+\mathcal{O}(\varepsilon)}{\partial \mathbf{z}(t)}+\mathcal{O}(\varepsilon) \\ &=-\mathbf{a}(t) \frac{\partial f(\mathbf{z}(t), t, \theta)}{\partial \mathbf{z}(t)} \end{aligned} \] 即证得
下一个证明使用了上面的结论,即最后求解 $ \(所用的积分等式。简单来说这里新定义了一个\) {aug}(t)$,使用上面的结果得到一个关于 $ {aug}(t)$的微分方程,再对t进行积分,即证明了该积分等式。 